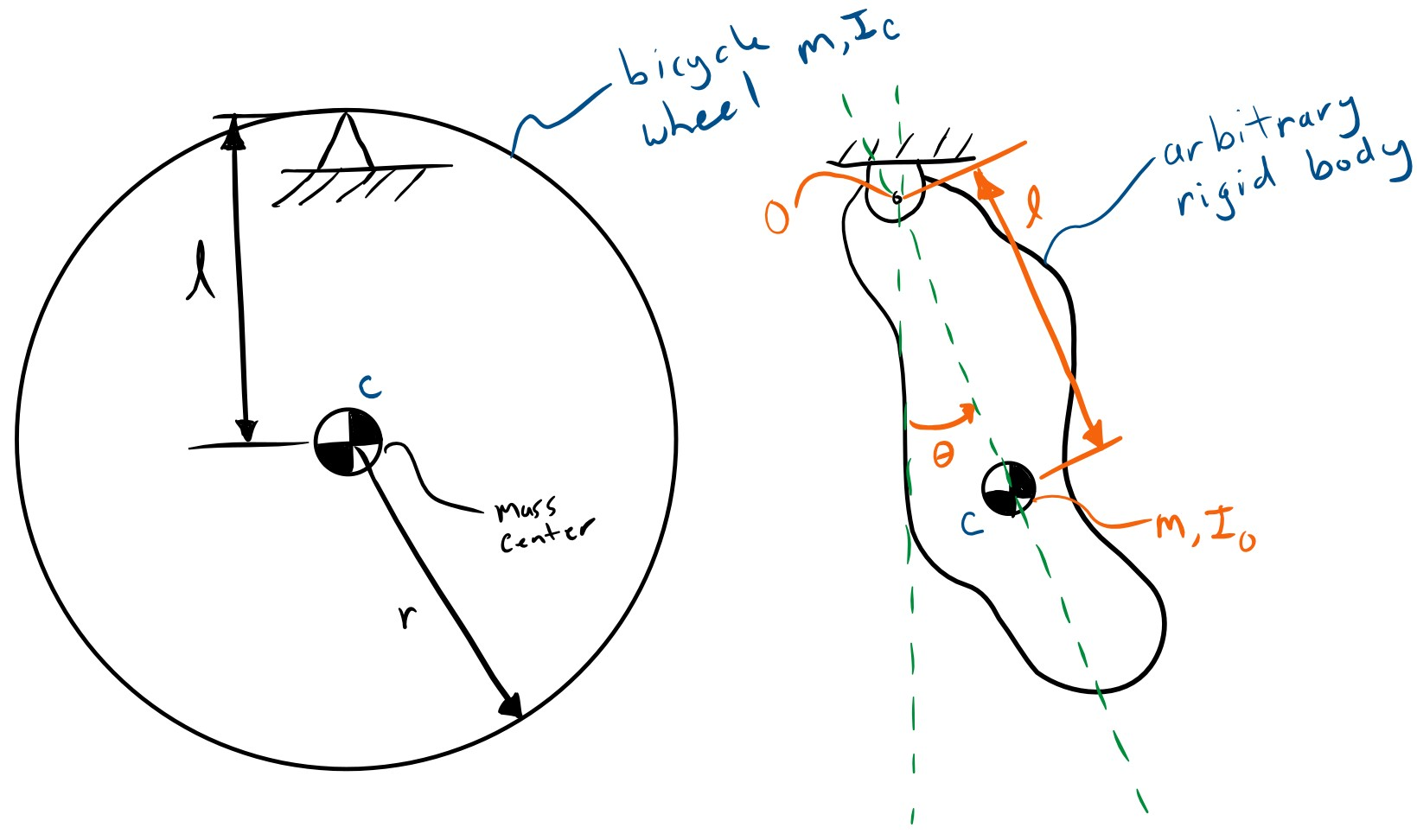
40 pendulum free body diagram

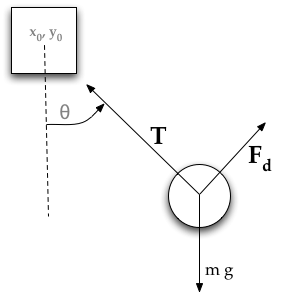
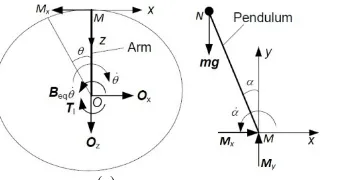
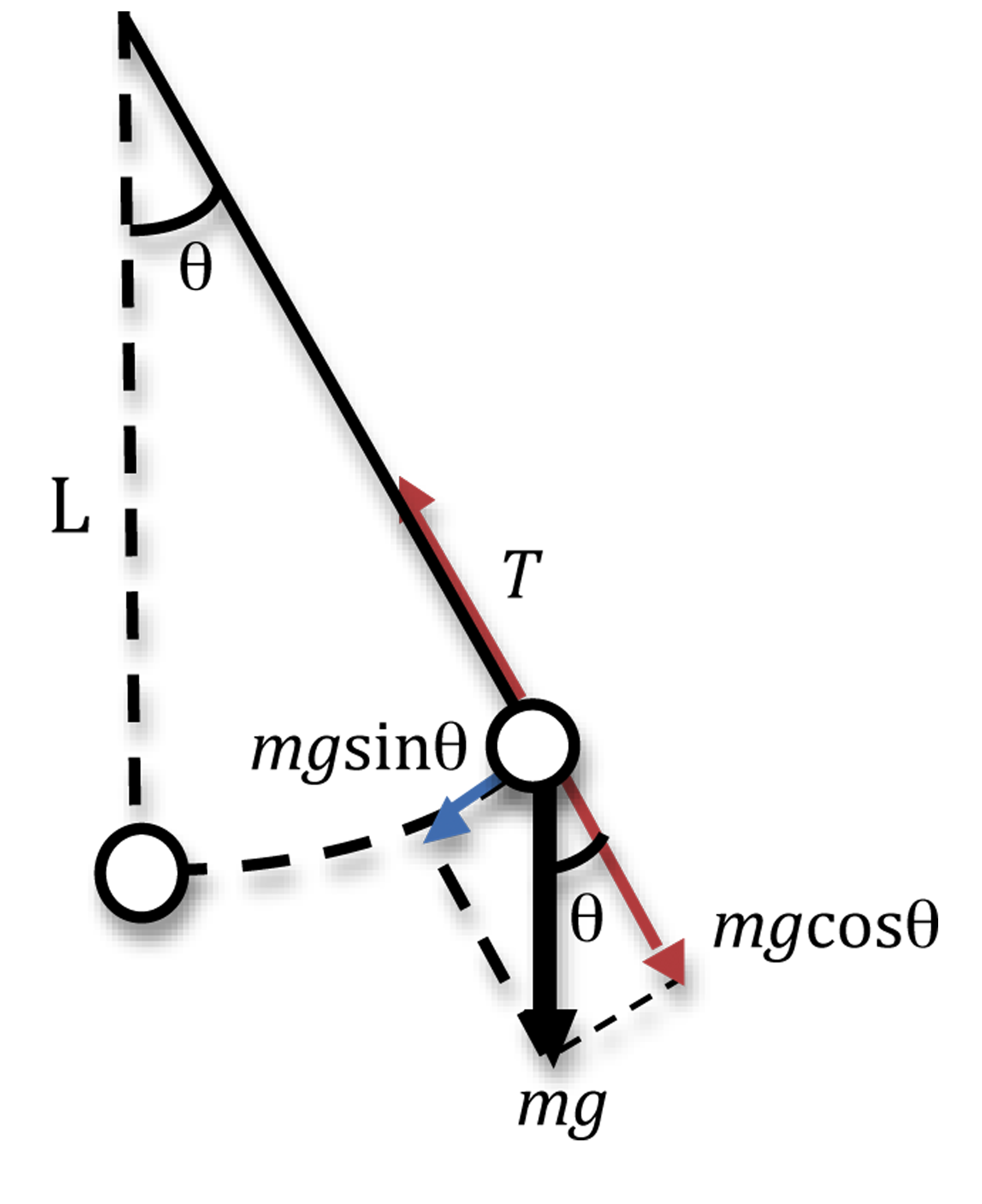
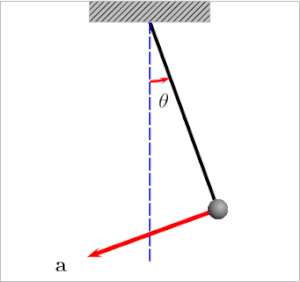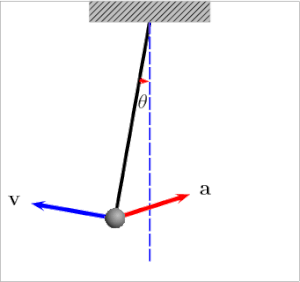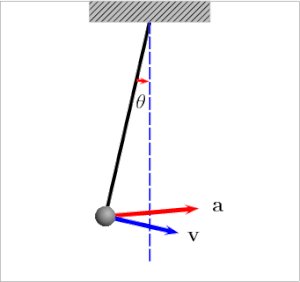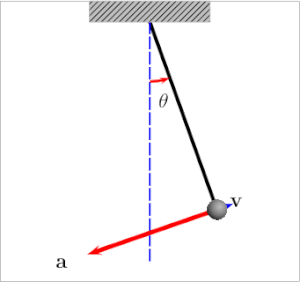
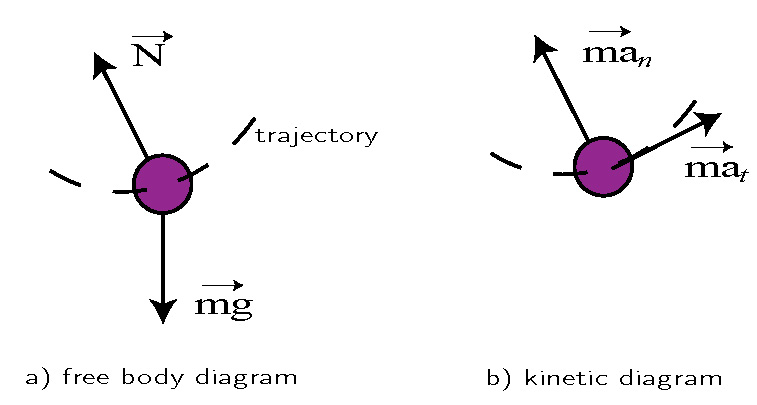
A pendulum is a body suspended from a fixed support so that it swings freely back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. The force of the gravity can be decomposed into two components; one is parallel to the pendulum or the tension, and one perpendicular [3], as shown in Fig. 1.

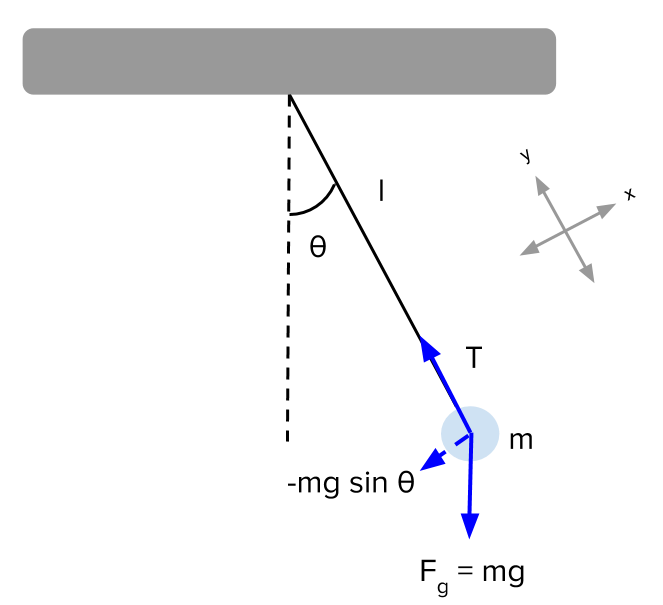
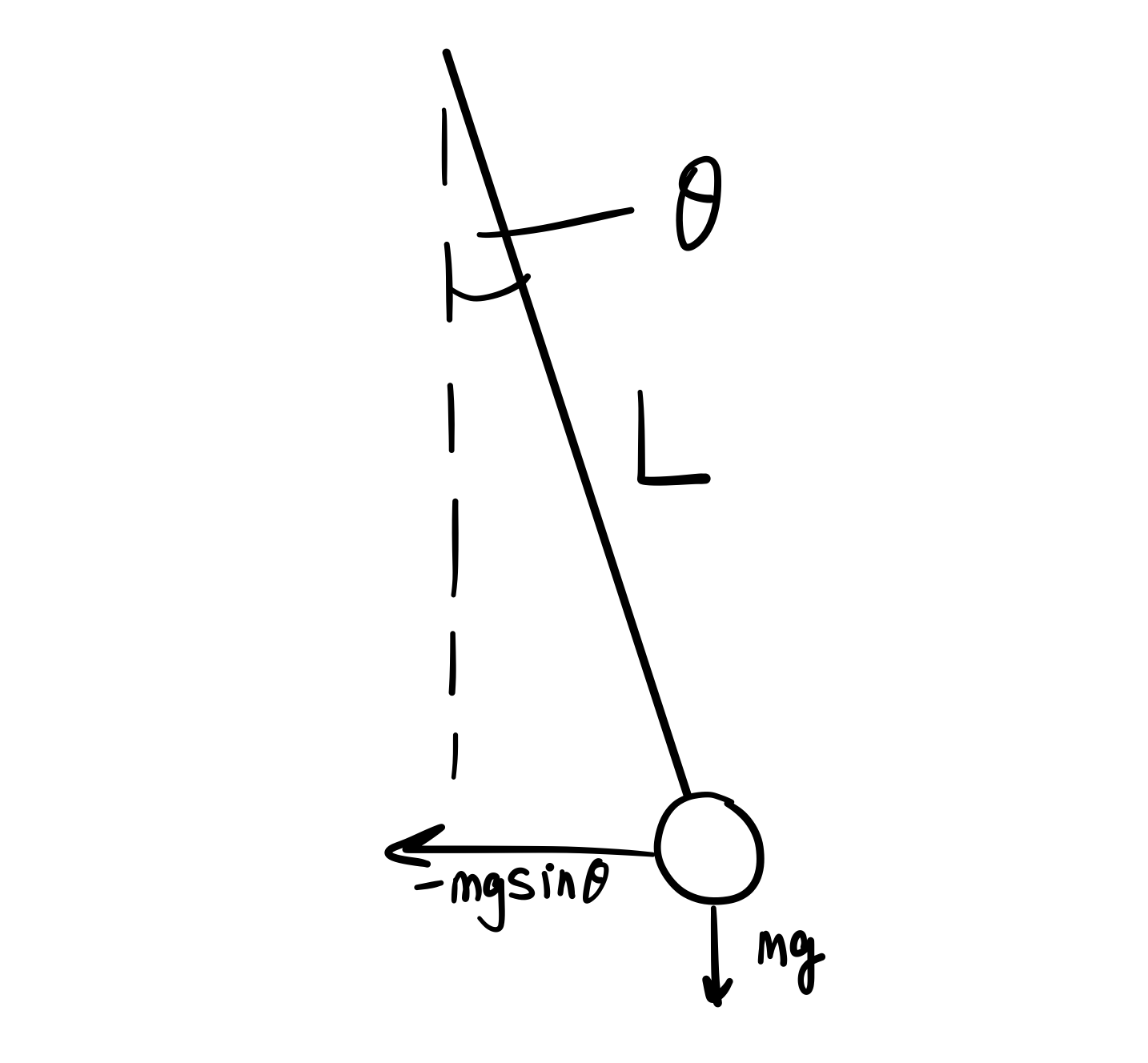
The free-body diagram is drawn in Figure 12.18). There is a downward force of gravity, and a force of tension directed away from the ball along the string.2 pages

Pendulum free body diagram

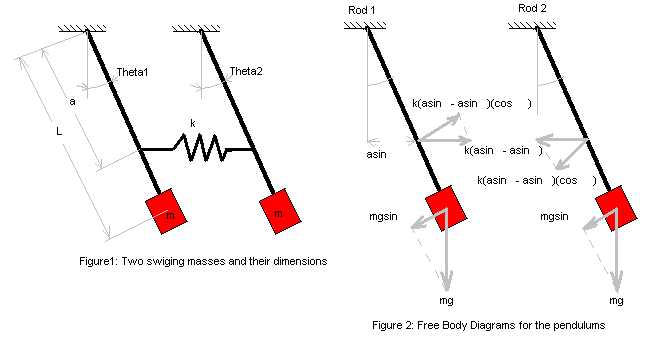
A simple pendulum consists of a relatively massive object - known as the pendulum bob - hung by a string from a fixed support. When the bob is displaced from equilibrium and then released, it begins its back and forth vibration about its fixed equilibrium position. The motion is regular and repeating, an example of periodic motion. In this Lesson, the sinusoidal nature of pendulum motion is ... Next we draw the free body diagram for the pendulum. The forces on the pendulum are the tension in the rod T and gravity. So we can write the net force as: F = T cos θ j − T sin θ i − m g j. Using Newton's law F = m a and the pendulum acceleration we found earlier, we have. Begin by drawing the free body diagram for the upper mass and writing an expression for the net force acting on it. Define these variables: T = tension in the rod; m = mass of pendulum; g = gravitational constant; The forces on the upper pendulum mass are the tension in the upper rod T 1, the tension in the lower rod T 2, and gravity −m 1 g ...

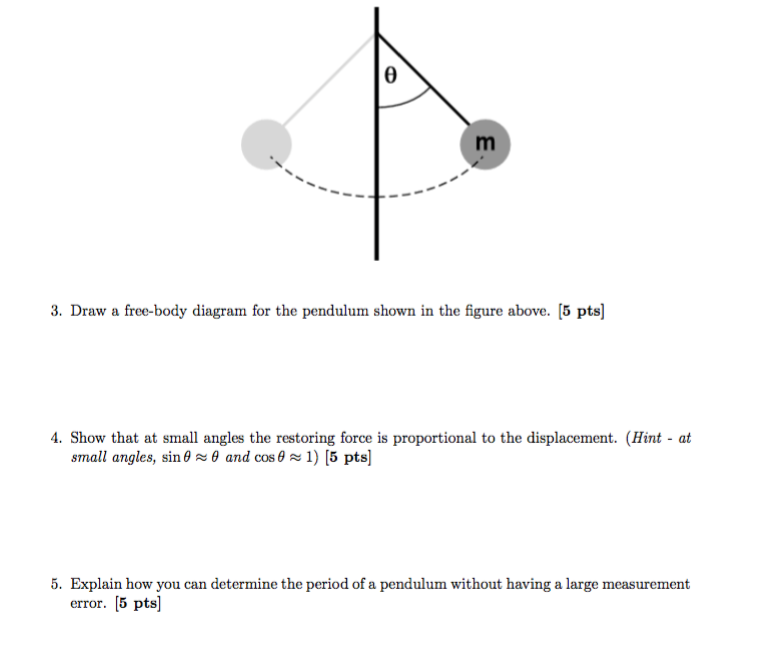
Pendulum free body diagram. Show a free body diagram of a pendulum while in equilibrium. View Answer. The steel bars AB and AC of the frame are pin-connected at the ends for buckling in the plane of the structure and Fixed ... 1 answerLet us consider the pendulum to be in simple harmonic motion, in this case, the restoring force, −mgsinθ − m g sin ⁡ θ acting on the bob of the pendulum is ... To begin, we first draw the free-body diagram where the forces acting on the pendulum are its weight and the reaction at the rotational joint. We also include a moment due to the friction in the joint (and the rotary potentiometer). No information is available for this page.Learn why

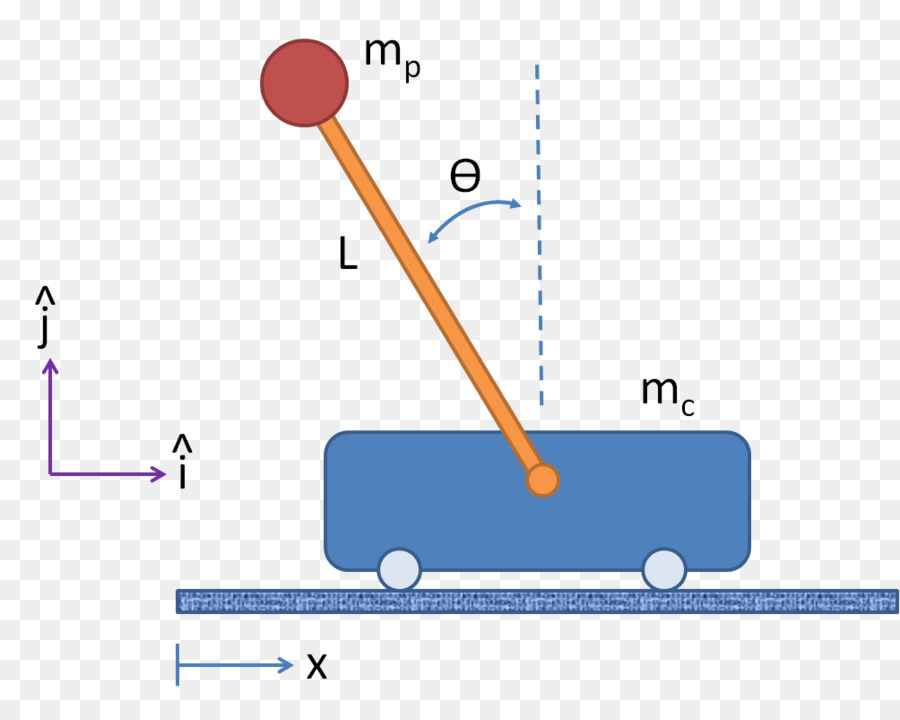
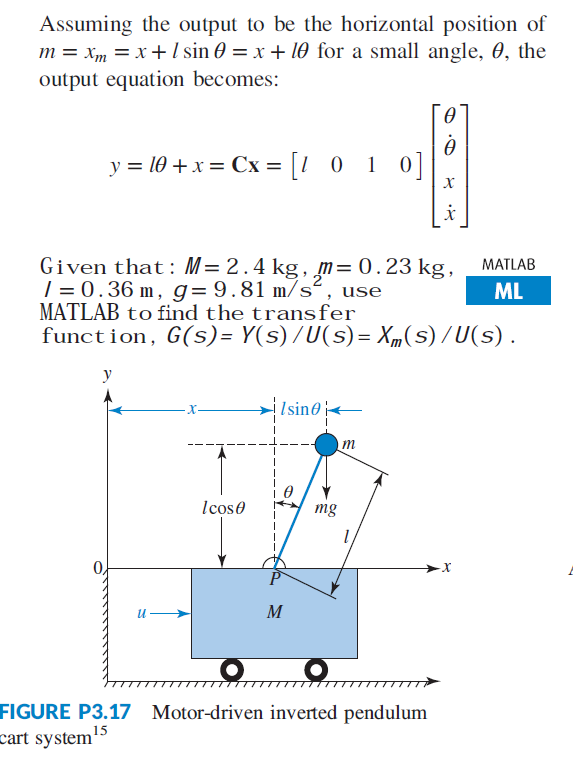
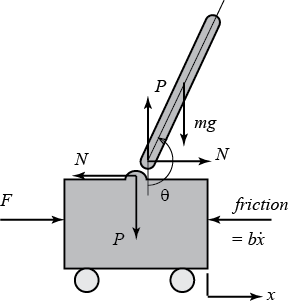
Below are the free-body diagrams of the two elements of the inverted pendulum system. Summing the forces in the free-body diagram of the cart in the horizontal direction, you get the following equation of motion. (1) Note that you can also sum the forces in the vertical direction for the cart, but no useful information would be gained. We'll call that its angular acceleration, since the pendulum is ... zoom in on the pendulum diagram and visualize those components of the gravity force:. The design requirements for the Inverted Pendulum state-space example are: Settling time for x and theta of less than 5 seconds. Rise time for x of less than 0.5 seconds. Overshoot of theta less than 20 degrees (0.35 radians). Force analysis and system equations. Below are the two Free Body Diagrams of … The force diagram on the pendulum is shown in Figure 24.4. In particular, there is an unknown pivot force and the gravitational force acts at the center of mass of the rod. Figure 24.4 Free-body force diagram on rod The torque about the pivot point P is given by P τ=r P,cm ×mg. (24.3.2)

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging ... Begin by drawing the free body diagram for the upper mass and writing an expression for the net force acting on it. Define these variables: T = tension in the rod; m = mass of pendulum; g = gravitational constant; The forces on the upper pendulum mass are the tension in the upper rod T 1, the tension in the lower rod T 2, and gravity −m 1 g ... Next we draw the free body diagram for the pendulum. The forces on the pendulum are the tension in the rod T and gravity. So we can write the net force as: F = T cos θ j − T sin θ i − m g j. Using Newton's law F = m a and the pendulum acceleration we found earlier, we have. A simple pendulum consists of a relatively massive object - known as the pendulum bob - hung by a string from a fixed support. When the bob is displaced from equilibrium and then released, it begins its back and forth vibration about its fixed equilibrium position. The motion is regular and repeating, an example of periodic motion. In this Lesson, the sinusoidal nature of pendulum motion is ...